快捷导航
上海总部:上海市 普陀区 怒江北路598号 红星世贸大厦B栋1206室
邮编:200333
总机:021-61243616
传真:021-61243616*819
业务邮箱:
sales@hmelectronics.com.cn
邮编:200333
总机:021-61243616
传真:021-61243616*819
业务邮箱:
sales@hmelectronics.com.cn
资讯文章
谐振直流环节变换器分析二
谐振直流环节变换器分析二
为了加深对ZVS物理过程的理解,下面用微分方程进行分析。
图12-5为谐振电路的简化等效电路。
假设负载电感远大于谐振电感Lr时,在一个谐振周期内可以认为负载电流Id不变。
图12-6为一个谐振周期的等效电路。
V截止时电感L中电流为iL,根据电压平衡关系
将式(12-2)代入式(12-1)得
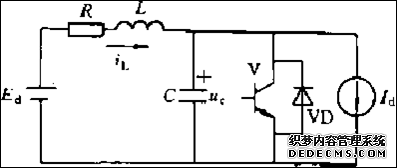
图12-6 一个谐振周期的等效电路
2阶微分方程解:
UC=Ed-IdR+ A1e-δtsinωt+A2e-δtcosωt (12-4)
式中 ω——谐振电路谐振角频率
ω2=ω02-δ2(12-5)
ω02=1/LC(12-6)
δ=R/2L(12-7)
根据起始条件定A1,A2系数
t=0 时iL=IL0 UC=0
得
A2=-Ed+IdR(12-9)
将式(12-8)和(12-9)代入式(12-4)得
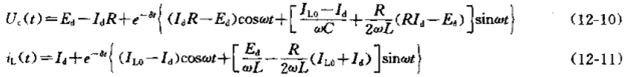
为了便于分析,在谐振电路中电阻R《ωL条件下除保留e-δt项之外,忽略R有关项。UC、iL可表示为
其中 Im=IL0 一 Id 为谐振电路歼始谐振时电感电流IL0与负载电流Id之差
令
则有
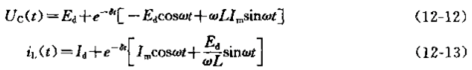
从式(12-14)可以看出Uc(t)是由恒定分量Ed叠加上幅值为√(Ed2+(ωLIm)2按e-δt衰戒的,以ω为角频率的正弦波。如果没有Im,就没有ωLIm项,Uc(t)总是大于零,谐振时UC将回不到零电压,也就无法进行ZVS操作,所以Im要保持一定值,就是说在谐振起始时电感中的电流IL0要比负载电流Id大一定的值。Im小了达不到请振后Uc(t)=0, Im大了又引起过电压。
Im最小值和谐振电路品质因数Q有关,如图12-7所示,Q小了Im最小值增大,电容电压峰值也增高。
(文/上海合美电子科技有限公司)
主营产品:三菱功率模块、Concept驱动、EV/HEV功率器件、SVG方案、光伏逆变器、三菱NewMPD、三菱电能质量、IGBT变频、三菱机车模块
